
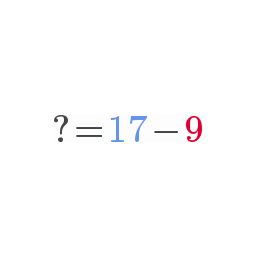

For this to happen, you must perform row operations to "pivot" along each entry along the diagonal. In your question, you say you reduce a matrix A to a diagonal matrix where every nonzero value equals 1. Here are some abbreviations to start off with:
Also, Gaussian elimination is all you need to determine the rank of a matrix (an important property of each matrix) while going through the trouble to put a matrix in reduced row echelon form is not worth it to only solve for the matrix's rank. However, Gaussian elimination in itself is occasionally computationally more efficient for computers. For small systems (or by hand), it is usually more convenient to use Gauss-Jordan elimination and explicitly solve for each variable represented in the matrix system. Gaussian Elimination helps to put a matrix in row echelon form, while Gauss-Jordan Elimination puts a matrix in reduced row echelon form.


 0 kommentar(er)
0 kommentar(er)
